Monitoring the training process in team sports

From description to prescription: Part 3

Athletes train to improve their performance, thereby exposing themselves to physiological, biomechanical and psychological loads. These loads need to be periodised carefully to achieve the desired performance at the right time. While individual athletes often peak to a short(er) competition period, team sport players’ performance need to be maintained throughout a long competitive season.

In this blog post, we discuss the relationship between load and performance, one of the three relationships that can be identified in the diagnostic stage of our roadmap to monitoring the training process in team sports.

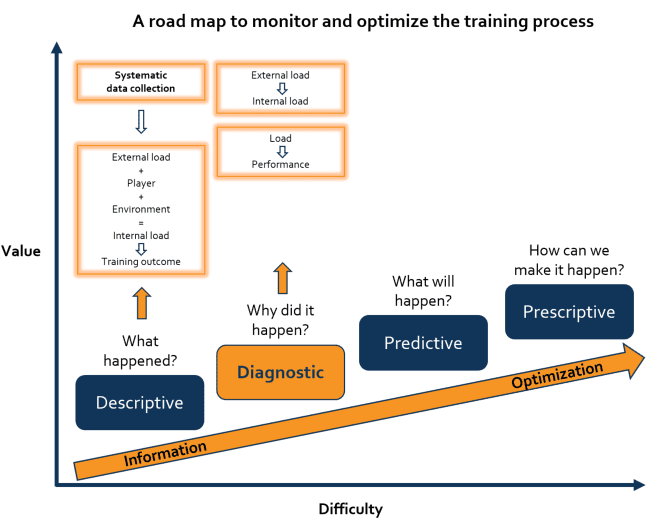
In our previous blog post, we have already mentioned the relation between load and performance by means of efficiency scores. These are based on ratios between external and internal load. As described by the aforementioned model of Impellizzeri and colleagues, the internal load is considered the ultimate stimulus for training adaptations and results from the interaction between the external load and the player characteristics. A given external load can, therefore, elicit a different internal load for each player within a team, thereby highlighting the need for individual training load prescription. Additionally, a player’s internal load response to a certain external load may also vary over time because of changes in performance capacity. Therefore, the relationship between external and internal load could be used to evaluate players’ adaptations to the training plan.

A performance-related training outcome can be positive (i.e. improved performance), neutral (i.e. maintenance of performance) or negative (i.e. decline in performance). The outcome is the result of the net balance between two antagonistic components: fitness (+) and fatigue (-) (Banister et al, 1975). These two components need to be balanced adequately to optimise the performance on a given time point. For example, if a player has not trained or played enough, a reduced or insufficient performance may be the consequence of a lower fitness level. On the other hand, when a player has a high training load or match load, the management of short-term fatigue is the main purpose for practitioners to ensure a good performance level. Therefore, it can be useful to quantify both fitness and fatigue components over time using the following formula:

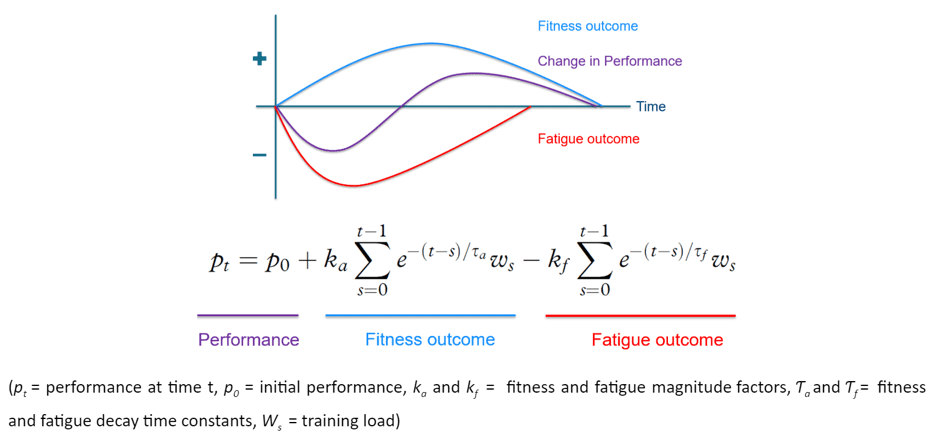
The application of this Banister impulse-response (IR) model is properly explained in a paper by Clarke and Skiba. For the application of this formula, it is important to understand the impact of the two factors (k and Ƭ) and to set these as good as possible. In brief, fitness can be considered as the ‘slow component’ (low k factor and high Ƭ factor) because fitness requires time to be improved. When you reach a certain fitness level and stop training, detraining (i.e. losing fitness) will generally occur after some weeks. In contrast to fitness, fatigue can be considered as the ‘fast component’ (high k factor and low Ƭ factor). For example, muscle soreness can be present just after heavy training but will often quickly disappear.

The fitness-fatigue model has proven its value in describing the relationship between load and performance in various sports. However, some limitations need to be mentioned. These are well described by Andrew Coggan.

First, it is difficult to exactly determine the value of the k and Ƭ factor. To explain the relationship between load and performance retrospectively, both factors can be determined using the best-fit approach (the combination of the k and Ƭ factor that delivers the highest accuracy of the model). However, to determine the current performance or predict future performance, the standard k and Ƭ factors (e.g. ka = 1, kf = 2, Ƭa = 28 and Ƭf = 7) are often not accurate enough.

Second, as proposed by Thierry Busso, a stable k and Ƭ factor may not be realistic as these factors may depend on the previous load exposure and corresponding fitness and fatigue states. Therefore, Busso proposes a fitness-fatigue model with time-varying k and Ƭ factors.

In conclusion, the fitness-fatigue model proposed by Banister et al. (1975) provides a useful estimation of the load-performance relationship and corresponding readiness status of players. The application of the fitness-fatigue model is also integrated into our own platform. However, the model has its limitations and cannot precisely determine the current status or predict future performance of a player. Therefore, practitioners often evaluate performance using standardised fitness and fatigue tests. We, therefore, advise a combination of performance modelling and testing to the performance of your players. In the following blog posts, we will provide more information about the current fitness and fatigue tests.